Working Theory Of A Half Wave Rectifier Circuit | Waveform | Mathematical Analysis

Rectifier

A rectifier is an electrical circuit or device that converts periodically reversing alternating current (AC) into unidirectional direct current (DC). Rectifiers have numerous applications, although they are most commonly encountered as components of DC power supplies and high-voltage direct current power transmission systems. Rectification can be used for purposes other than generating direct current for use as a power source. There are two types of rectifier circuits: 1) Half wave rectifier and 2) Full wave rectifier.

Half Wave Rectifier

When a AC waveform is applied and when half of the AC cycles gets rectified, it is called as half wave rectifier. The output voltage of the half wave rectifier is not pure DC as the AC components are present in this voltage. This AC component is called as ripple voltage. In half wave rectification, the rectifier only conducts during the positive half cycles of the alternating current (AC) supply. During negative half cycles, no current is conducted, and as a result, there is no voltage across the load.

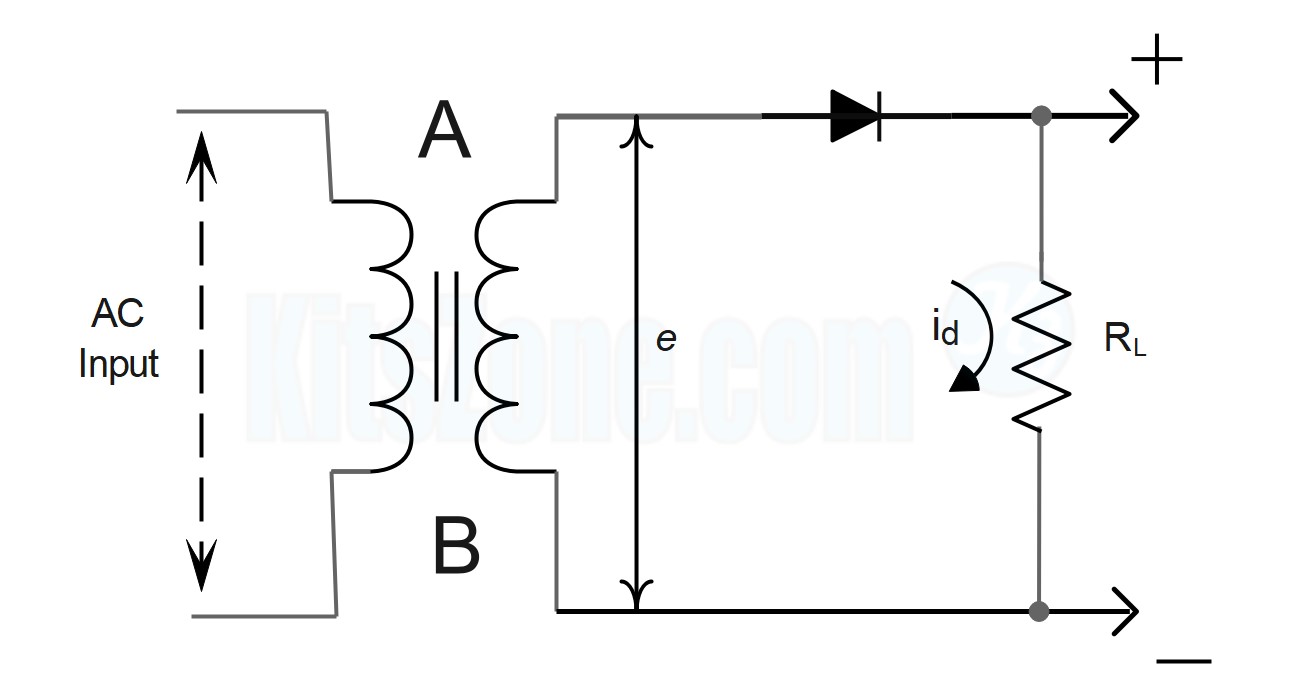
Circuit Diagram

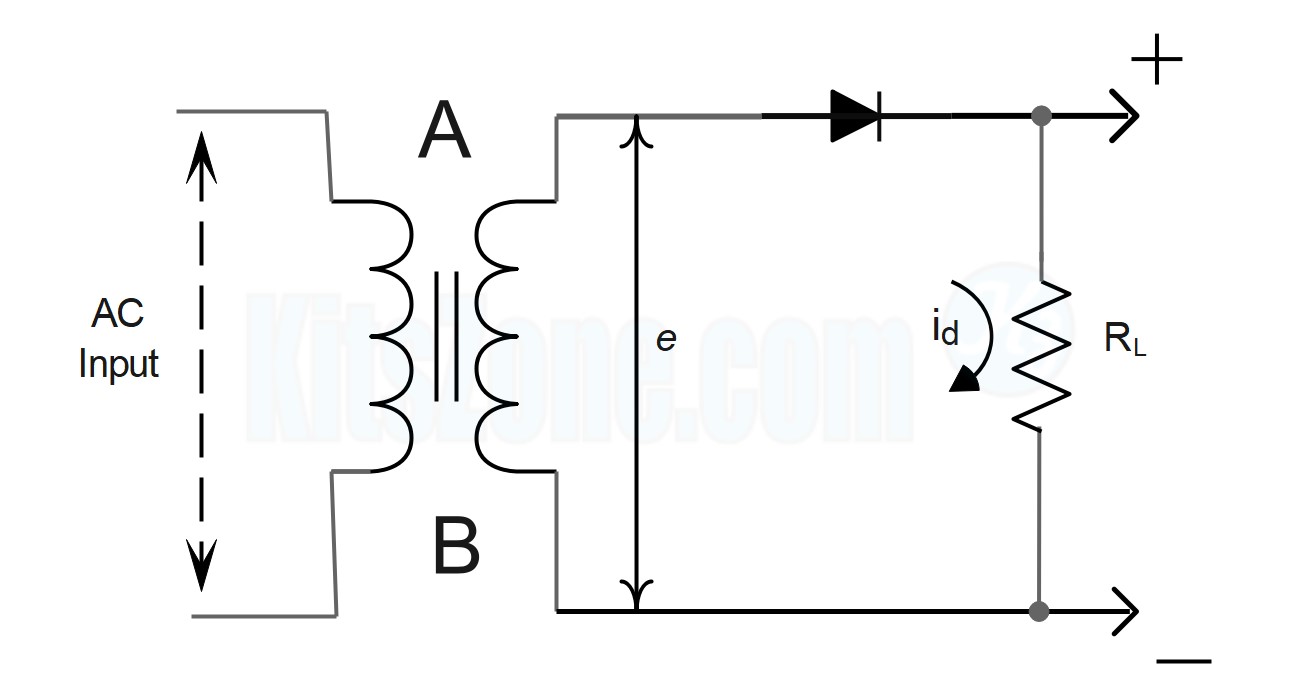
Circuit Details

In the circuit presented above, a single diode functions as a half-wave rectifier. The to-be-rectified AC supply is connected in series with the PN junction diode and a load resistance R_L. In this experiment, the AC supply is obtained through a transformer. The use of transformer offers two benefits. 
First, it allows us to increase or decrease the AC voltage depending on the circumstances using a step up or step down transformer.
The transformer also isolates the rectifier circuit from the power line, reducing the risk of electric shock.

Circuit Working

A is positive with respect to B when an AC supply is applied to the input circuit during one half of the cycle. This makes the diode's P terminal positive with respect to its N terminal. Consequently, the diode is forward biased, and current travels through the load R_L in the direction depicted in the circuit above. During the subsequent half-cycle, the point A is negative relative to point B. Consequently, the diode is reverse biased and does not conduct (except for a very small reverse current which is negligible), so no current flows through the load R_L. 
The diode conducts during the positive half cycle and does not conduct during the negative half cycle. Thus, when an AC signal is applied to the input of the rectifier, only one-directional current flows through R_L. The output across R_L will therefore be a DC. The wave forms of the input and output are shown below. As the output comprises only the positive half of the input wave, this rectifier is referred to as a half-wave rectifier.

Input And Output Waveform

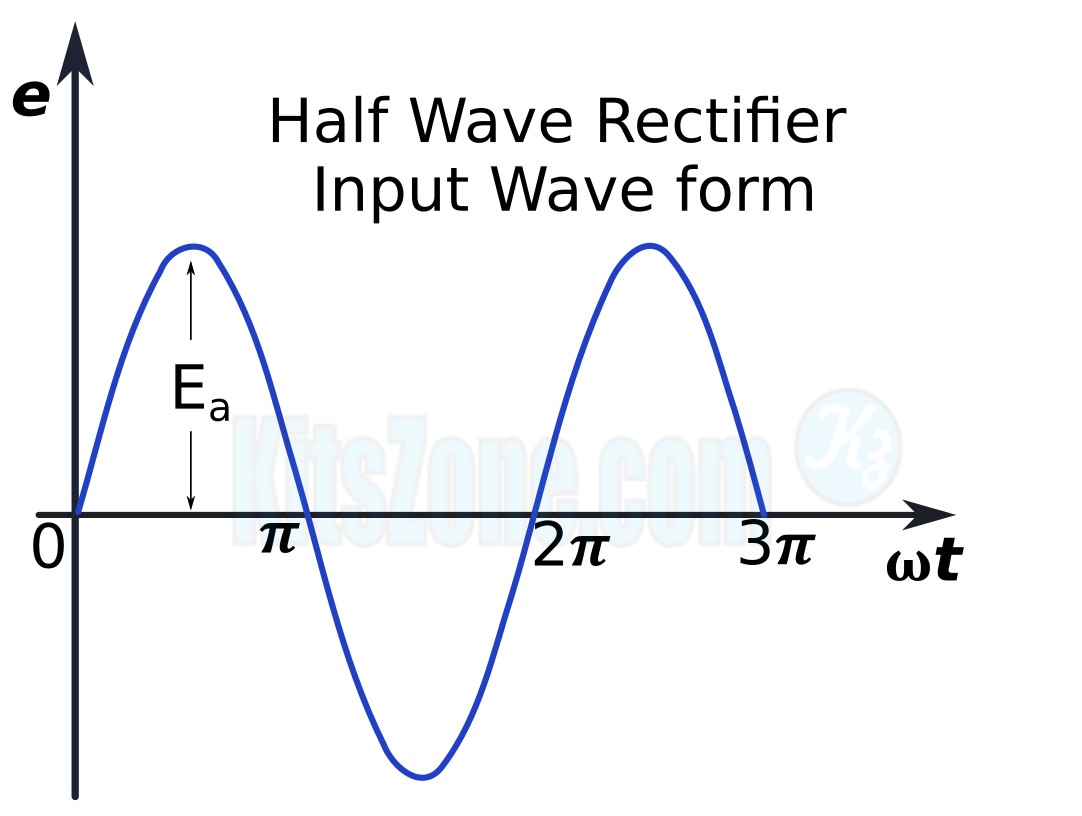
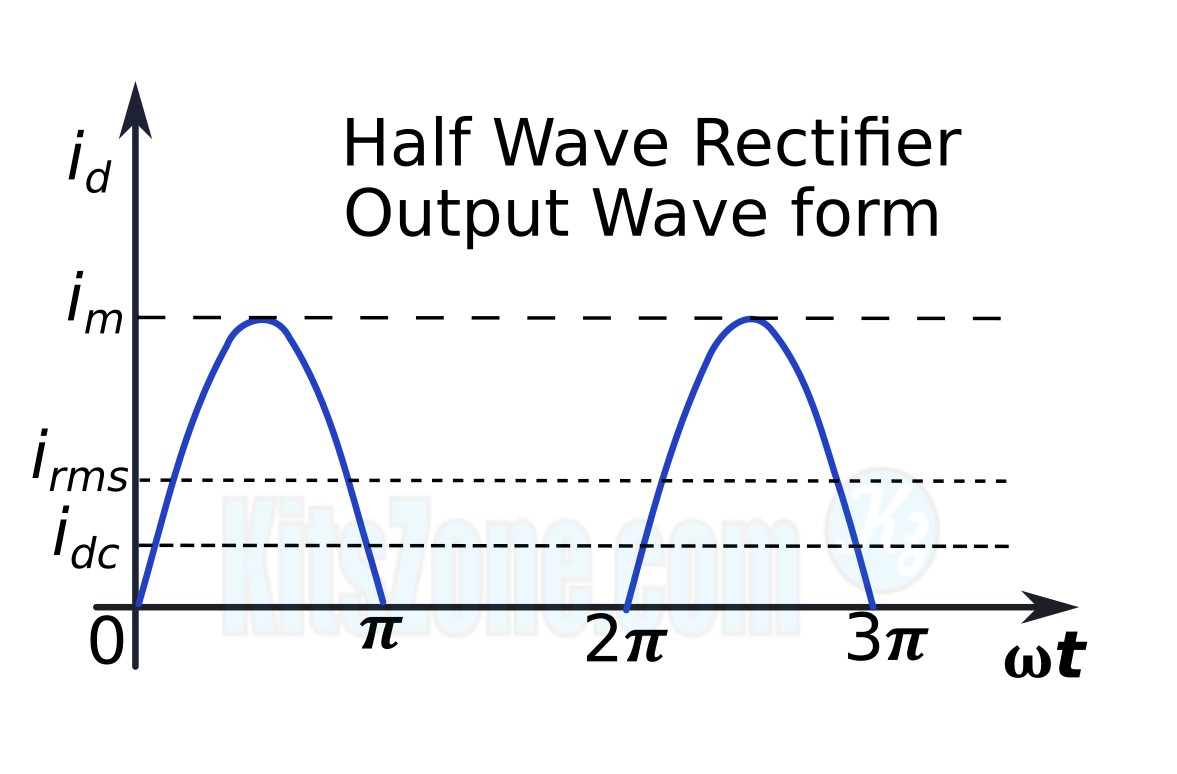
Mathematical Analysis

Let  e = E₀ + sin wt  be the input voltage to the rectifier, where E₀  be the peak input voltage. When the diode is conducting, let i_d  be the current flowing through the circuit and let the voltage drop across the diode be e_d.

Assuming the ohmic resistance of the secondary of the transformer as negligible and applying Kirchhoff's voltage law to this circuit we have,

\[\begin{array}{l}
e = {e_d} + {i_d}{R_L}\\
 = {i_d}{R_f} + {i_d}{R_L}
\end{array}\]

Where R_f is the forward dynamic resistance of the diode.

\[\begin{array}{l}
\therefore e = {i_d}({R_f} + {R_L})\\
i.e.,{E_o}\sin \omega t = {i_d}({R_f} + {R_L})\\
i.e.,{i_d} = {i_m}\sin \omega t\\

\end{array}\]

\[{\text{where }}{i_m} = \frac{{{E_o}}}{{{R_f} + {R_L}}}{\text{is the peak current}}{\text{.}}\]

If the resistance of the diode is negligible compared to R_L, then

\[{i_m} = \frac{{{E_o}}}{{{R_L}}}\]

For a half wave rectifier, we have, (Refer the second graph)

\[{i_d} = \left\{ {\begin{array}{*{20}{c}}
  {\sin \omega t}&{{\text{for }}0 < \omega t < \pi } \\ 
  0&{{\text{for }}\pi  < \omega t < 2\pi } 
\end{array}} \right.\]

DC Value Of Current(I_dc)

From the second graph, it can be noticed that the output current is not steady but contains fluctuations despite of being a DC current. The average value of this fluctuating DC current can be calculated as follows:

$$\eqalign{
  & {{\text{I}}_{dc}} = \frac{1}{{2\pi }}\int_0^{2\pi } {{{\text{I}}_d}} d(\omega t)  \cr 
  &  = \frac{1}{{2\pi }}\left[ {\int_0^\pi  {{i_d}} d(\omega t) + \int_\pi ^{2\pi } {{i_d}} d(\omega t)} \right]  \cr 
  &  = \frac{1}{{2\pi }}\int_0^\pi  {{i_d}} d(\omega t)\,\,\,\,\,\,\,\,\,\,\,\,{\text{ }}\left[ {\because {i_d} = 0{\text{ in the range }}\pi {\text{ to 2}}\pi } \right]  \cr 
  &  = \left( {\frac{1}{{2\pi }}} \right)\int_0^\pi  {{{\text{I}}_m}} \sin \omega t{\text{ }}d(\omega t)  \cr 
  &  = \frac{{{{\text{I}}_m}}}{{2\pi }}\left[ { - \cos (\omega t)} \right]_0^\pi   \cr 
  & \therefore {{\text{I}}_{dc}} = \frac{{{\operatorname{I} _m}}}{\pi } \cr} $$

RMS Value Of A Current (I_rms)

$$\eqalign{
  & {{\text{I}}_{rms}} = \sqrt {\frac{1}{{2\pi }}\int_0^{2\pi } {i_d^2d\left( {\omega t} \right)} }   \cr 
  &  = \sqrt {\frac{1}{{2\pi }}\left[ {\int_0^\pi  {i_d^2d\left( {\omega t} \right)}  + \int_\pi ^{2\pi } {i_d^2d\left( {\omega t} \right)} } \right]}   \cr 
  &  = \sqrt {\frac{1}{{2\pi }}\int_0^\pi  {i_d^2d\left( {\omega t} \right)} } \,\,\,\,\,\,\,\,\,\left[ {\because {i_d} = 0{\text{ in the range }}\pi {\text{ to }}2\pi } \right]  \cr 
  &  = \sqrt {\frac{1}{{2\pi }}\int_0^\pi  {I_m^2{{\sin }^2}\omega t{\text{ }}d\left( {\omega t} \right)} }   \cr 
  &  = \sqrt {\frac{{I_m^2}}{{2\pi }}\left[ {\frac{{\omega t}}{2} - \frac{{\sin 2\omega t}}{4}} \right]_0^\pi }   \cr 
  &  = \sqrt {\frac{{I_m^2}}{{2\pi }}\frac{\pi }{2}}   \cr 
  &  = \sqrt {\frac{{I_m^2}}{4}}   \cr 
  & \therefore {{\text{I}}_{rms}} = \frac{{{I_m}}}{2}  \cr 
  & \therefore {{\text{I}}_{rms}} > {{\text{I}}_{dc}} \cr} $$

Efficiency (η)

$$\eqalign{
  & \eta  = \frac{{{\text{Output DC Power}}}}{{{\text{Input AC Power}}}} \times 100\%   \cr 
  & {\text{Let Input AC Power  = }}{{\text{P}}_{iac}}  \cr 
  & {{\text{P}}_{iac}} = \frac{1}{{2\pi }}\int_0^{2\pi } {\left( {{\text{instantaneous power}}} \right)} {\text{ d}}\left( {\omega t} \right)  \cr 
  & {{\text{P}}_{iac}} = \frac{1}{{2\pi }}\int_0^{2\pi } {e \times {i_d}} {\text{ d}}\left( {\omega t} \right)  \cr 
  &  = \frac{1}{{2\pi }}\int_0^{2\pi } {{i_d}\left( {{R_f} + {R_L}} \right) \times {i_d}} {\text{ d}}\left( {\omega t} \right)  \cr 
  &  = \frac{{\left( {{R_f} + {R_L}} \right)}}{{2\pi }}\int_0^{2\pi } {i_d^2} {\text{ d}}\left( {\omega t} \right)  \cr 
  &  = \left( {{R_f} + {R_L}} \right){\text{I}}_{rms}^2  \cr 
  & \therefore {{\text{P}}_{iac}} = \frac{{\left( {{R_f} + {R_L}} \right){\text{I}}_m^2}}{4} \cr} $$

_________________

$$\eqalign{
  & {\text{Output DC Power }}{{\text{P}}_{odc}} = {\text{I}}_{dc}^2{{\text{R}}_L}  \cr 
  & {{\text{P}}_{odc}} = \frac{{{\text{I}}_m^2{{\text{R}}_L}}}{{{\pi ^2}}}  \cr 
  & \therefore {\text{Rectifier Efficiency }}\eta {\text{ = }}\frac{{{{\text{P}}_{iac}}}}{{{{\text{P}}_{odc}}}} \times 100\%   \cr 
  &  = \frac{{{\text{I}}_m^2{{\text{R}}_L}}}{{{\pi ^2}}} \times \frac{4}{{\left( {{{\text{R}}_f} + {{\text{R}}_L}} \right){\text{I}}_m^2}} \times 100\%   \cr 
  &  = \frac{{40.6{R_L}}}{{{{\text{R}}_f} + {{\text{R}}_L}}}\%   \cr 
  & {\text{If }}{{\text{R}}_f} <  < {{\text{R}}_L},{\text{ }}\eta {\text{ = 40}}{\text{.6}}\%   \cr 
  & {\text{If }}{{\text{R}}_f} = {{\text{R}}_L},{\text{ }}\eta {\text{ = 20}}{\text{.3}}\%  \cr} $$

Ripple Factor(r)

At the output of half wave rectifier, periodically varying components are still present even though we have achieved a unidirectional current. Filters are used in the rectifier to reduce the varying components. A measure of the varying component is given by the ripple factor as follows:

\[r = \frac{{{{I'}_{rms}}}}{{{I_{dc}}}} = \frac{{{{E'}_{rms}}}}{{{E_{dc}}}}\]

where I^'_rms and E^'_rms represent the RMS value of ripple current and voltage respectively.

Instantaneous value of ripple current I^' = i_d – I_dc

$$\eqalign{
  & {I^{\rm{'}}}_{rms} = \sqrt {{1 \over {2\pi }}\int\limits_0^{2\pi } {i{\rm{'}}_d^2d\left( {\omega t} \right)} }   \cr 
  &  = \sqrt {{1 \over {2\pi }}\int\limits_0^{2\pi } {{{\left( {{i_d} - {I_{dc}}} \right)}^2}d\left( {\omega t} \right)} }   \cr 
  &  = \sqrt {{1 \over {2\pi }}\int\limits_0^{2\pi } {{{\left( {i_d^2 - 2{i_d}{I_{dc}} + I_{dc}^2} \right)}^2}d\left( {\omega t} \right)} }  \cr} $$

\[\begin{array}{l}I_{rms}^' = \sqrt {\frac{1}{{2\pi }}\int\limits_0^{2\pi } {i{{_d^'}^2}d\left( {\omega t} \right)} } \\ = \sqrt {\frac{1}{{2\pi }}\int\limits_0^{2\pi } {{{\left( {{i_d} - {I_{dc}}} \right)}^2}d\left( {\omega t} \right)} } \\ = \sqrt {\frac{1}{{2\pi }}\int\limits_0^{2\pi } {{{\left( {i_d^2 - 2{i_d}{I_{dc}} + I_{dc}^2} \right)}^2}d\left( {\omega t} \right)} } \end{array}\]

\[\therefore I'_{m}=\sqrt{\frac{1}{2\pi}\int_{0}^{2\pi}{i}\{'}_{2}^{d}}\left(\omega t\right)\]

\[\therefore I'_{m}=\sqrt{\frac{1}{2\pi}\int_{0}^{2\pi}{i}\'_{d}^{2}\left(\omega t\right)\]

Using equations below

$$\eqalign{
  & {I_{dc}} = \frac{1}{{2\pi }}\int_0^{2\pi } {{I_d}d\left( {\omega t} \right)}   \cr 
  & \&   \cr 
  & {I_{rms}} = \frac{1}{{2\pi }}\int_0^{2\pi } {i_d^2d\left( {\omega t} \right)}  \cr} $$

we have

Ripple factor is given by

The above calculation shows that the RMS value of the ripple exceeds that of the DC potential of the output. This shows that the half wave rectifier without a filter is relatively a poor device for converting AC into DC.

Peak Inverse Voltage

It is defined as the maximum voltage applied across the diode when the diode is reverse biased. In the case of half wave rectifier, the maximum voltage across the diode when it is not conducting is equal to E₀, the peak input voltage.